10ticks Friday Puzzle

Welcome to Ian’s Friday Puzzle! Dust off those Friday cobwebs with a little manipulation of the old grey matter. Perplexing puzzles, logical, illogical, and sometimes just plain stupid. Be prepared to be bewildered, befuddled and bedazzled!
See the latest Friday Puzzle below and look at all the past puzzles. Get the Friday Puzzle straight to your phone, follow us on Twitter. The first 5 correct answers join our Hall of Fame!
This week's Friday Puzzle
Some grapes weighing 1 kg are 99% water.
They are left in the sun for a while and some water evaporates.
Now only 98% of the new weight is water.
What is the new weight of the grapes?
Friday Puzzle (08/12/2023)
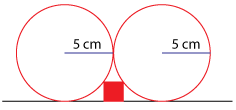
Find the area of the square.
Friday Puzzle (01/12/2023)
Place the whole numbers 1 to 8 in the squares so that the totals of each line of three is 15.
Friday Puzzle (24/11/2023)
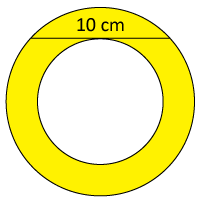
The 10 cm line is a tangent to the inner circle of the two concentric circles.
Find the yellow area.
Friday Puzzle (17/11/2023)
Martha has some marbles. She lays them out in equally spaced lines to form a square lattice.
She finds she needs 50 more marbles to complete the square lattice.
Mum, by mistake, buys her 150 more marbles.
By luck she is able to use every single marble she now has to complete a square lattice made of equally spaced lines.
How many marbles are in her final square?
Friday Puzzle (10/11/2023)
Find the digits A, B, C so that 5555ABC is a perfect square.
No calculators!
(A, B, C are the hundreds, tens and ones digits of the number).
Friday Puzzle (03/11/2023)
4 ⊕ 2 = 2682
6 ⊕ 3 = 29183
8 ⊕ 4 = 212324
What is 12 ⊕ 4 equal to?
Friday Puzzle (27/10/2023)
Which is bigger 3100 or 475?
Friday Puzzle (13/10/2023)
Jim has some biscuits.
He can share them among his x friends in two ways.
7 biscuits each with 2 left over, or 6 biscuits each with 7 left over.
How many biscuits does Jim have?

